Note: This is an automated translation (using DeepL) of the original German article.
The exponential function is a super explanatory model - but no good for actually predicting the pandemic
One of the many challenges in the current COVID-19 epidemic is to explain the credibility of the simulation models used. Since these models are highly complex computer programs, this is inherently anything but straightforward. Therefore, various models, often very simple in approach, are regularly used for this purpose - also called metamodels among modelers. These models perfectly represent certain mechanisms and dynamics of the real system and are thus ideally suited for the communication of effects. Unfortunately, such models are often misinterpreted and wrongly used for forecasting.
The exponential function is a great example of such a metamodel, as it perfectly characterizes the basic propagation dynamics of an epidemic. It has been widely used for this purpose since the epidemic began in the spring, but unfortunately it has been misunderstood at least as much: “You should have seen it coming,” many researchers said to themselves in November 2020 when they became aware of an exponential trend in case numbers since the summer. Indeed, the exponential trend was readily visible and evident, but could the explosion in case numbers in October really have been predicted with an exponential curve?
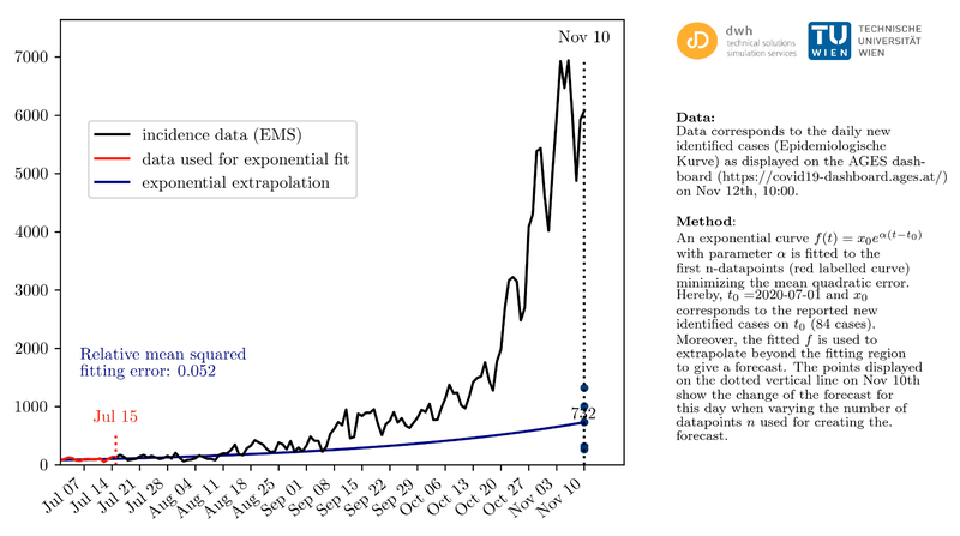
The video below shows an exponential model (blue curve), which is incorrectly used here for long-term forecasting. The model is fed, day by day, with the respective available “new” daily data (red line). For comparison, the actual epidemic progression (black curve) is shown.
Video: It is clear that the exponential function cannot be used to predict the epidemic.
You can see an exponential function alone would not have been able to predict plausible numbers of cases. The trend in October is clearly different from that in summer. But: It is doubtful whether any model would have been able to predict this trend so early. One reaches here the limits of forecasting (see remark below).
Note:
This example, with the goal to illustrate the use of an exponential function to simulate the epidemic, was already calculated in November 2020. Due to the current public discourse it was (re-)published in this form with additional information on January 18th, 2021.
Remark:
While a simple exponential model is useful as an illustrative example to explain the spreading dynamics of epidemics, more complex dynamic models are needed to make true forecasts. These have mechanisms that allow them to represent more complex dynamics. Nevertheless, even the best complex model is strongly bound to certain constraints for forecasting case numbers. For example, human behavior and future actions are virtually unpredictable. Thus, similar to weather forecasting, one to a maximum of two weeks is usually the limit for what can be plausibly predicted.